In this post I will briefly explain how the Quantum Approximate Optimization Algorithm works and how it provides approximate solutions to Combinatorial Optimization Problems like MaxCut. If these terms are not familiar to you, this blog will at least briefly and mathematically go through these elementary concepts and build upon them, as for me it took some time to read the paper iteratively to understand why it works. This blog requires that the reader has knowledge about the elementary concets in Quantum Computation, up until some widely known algorithms like Grover’s search or Shor’s factoring algorithm. I have referred to some great blogs and videos which will be pointed out in the blog and are detailed in the References.

In order to make the overall post not very lengthy, some parts are linked with expandable sections - like this one.

---

This is how the details would appear.

---

What kinds of problems are we targeting?

The Quantum Approximate Optimization Algorithm (QAOA) [1] aims to find an approximate solution to Combinatorial Optimization problems on Quantum Computers. One example of a Combinatorial Optimization problem is the MaxCut problem. The MaxCut problem involves finding a cut of a graph - which essentially means partitioning a graph into two sets of vertices, such that the number of edges passing through the two sets is maximized. It is an NP-Complete problem.

---

Combinatorial Optimization problems - these problems where one has to optimize a function by choosing an element from a finite set of elements such that the value of the function on that element is maximized or minimized according to what the objective is. See this for more details.

---

---

What are NP, NP-Complete and NP-Hard problems?
In Computer Science, there are exist some problems that are "easily" solvable. By "easy", we mean that the problem can be solved in polynomial time i.e. O(n^k), where n is the size of the problem and k is some constant. For our purposes, we require 4 classes:

P - this is a class of problems for which there are known algorithms that solve the problem in Polynomial time.

NP - this is a class of problems for which there are no known algorithms that solve the problem deterministically in polynomial time. There may exist randomized algorithms that in some case might take a polynomial time path to reach a solution. Thus non-deterministic polynomial time algorithms may exist, which is also what NP stands for. (Non-deterministic polynomial, and not non-polynomial). Another point to note is that if a solution to an NP problem is provided, it can be verified by an algorithm in polynomial time.

NP-Hard - this is a class of problems which are "harder" than NP problems. The term "hard" refers to generalization, which essentially means that all problems in the set NP are special cases of NP-Hard problems. The first NP-Hard problems of SAT and 3-SAT problems were proved to be NP-Hard by hand. Generally, to prove that any problem is NP-Hard, one needs to prove that an existing NP-Hard problem is a special case of the problem at hand.

NP-Complete - this is a class of problems which are both NP-Hard and in NP.

---

The MaxCut Problem

The authors of QAOA used the MaxCut problem to demonstrate the algorithm and to demonstrate some proofs. As an example that I will use throughout this blog, consider the following simple 3 node graph.

The solution to this problem would be the cut shown in Figure 2, where V₁ is in one group and V₂, and V₃ are in the other.

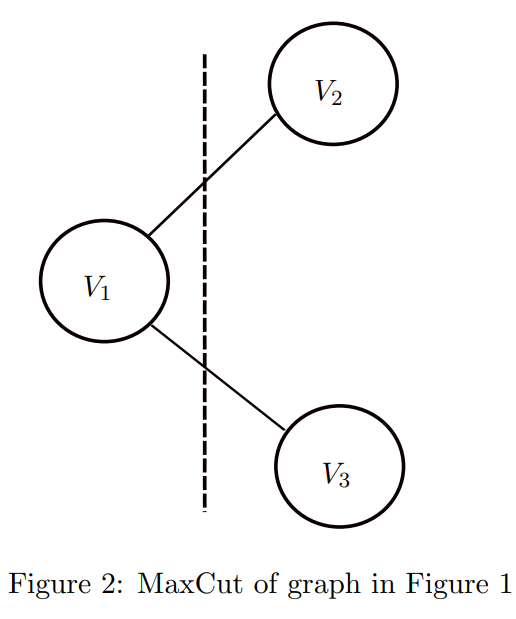
The value of this cut is 2. Following are the values of other non-zero valued cuts in the graph. Note that the total number of cuts in a general graph is of the order 2^|V|.

A: {V₁}, B: {V₂, V₃}: Cut Value: 2

A: {V₂}, B: {V₁, V₃}: Cut Value: 1

A: {V₃}, B: {V₁, V₂}: Cut Value: 1

Description of QAOA on MaxCut

The algorithm would first require some mathematical notations to describe the problem and the solution. QAOA assigns a qubit to each vertex of a given graph G. Hence, on performing a measurement, the result would be one of the computational basis states, which would represent a candidate solution.

In the following table, the qubit order is \(\\|q_1q_2q_3\rangle\)

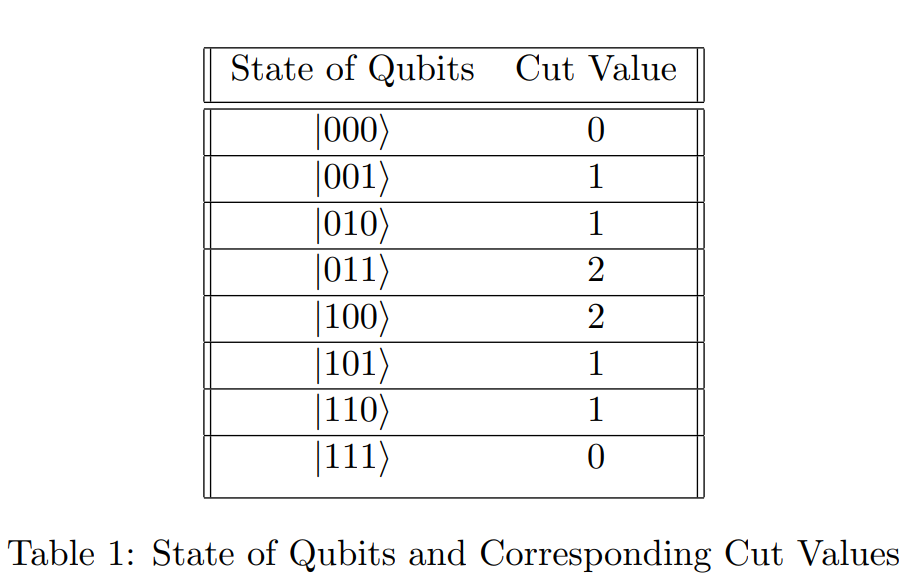
Due to the objective of this problem (maximization), let there be a Cost function that needs to be maximized. A cost function generally has a candidate solution as an input and the value of the candidate solution as the output. Thus, in the case of MaxCut, the input would be any possible cut, and the output would then be the number of edges crossed between the two sets of vertices in the cut. The left column in Table 1 would be the input and the right column would represent the corresponding outputs of such a function. The way such a Cost function is represented in many Quantum Algorithms is through something called a Hamiltonian.

---

When a Quantum Gate is applied to a state of qubits, they are transformed into a new state. In general, the Hamiltonian of a system describes how a Quantum System evolves over time. The matrix representation of the Hamiltonian is Hermitian, which means that it is diagonalizable. In physical systems, the eigenvalues of the system represent energy, and the eigenstates represent the different enery levels corresponding to these energies. The ground state corresponds to the eigenstate having the lowest eigenvalue. Additionally, if the state at time 0 is in one of the eigenstates of the Hamiltonian, then applying the Hamiltonian will give back the same state and the state will stop evolving. See this for a detailed explanation.

---

Now, for the example that we took (Figure 1 and Table 1), consider the following matrix representation of a Hamiltonian:

\[\begin{equation}\label{exampleProblemHamiltonian} \hspace{20pt} \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Taking a closer look at this matrix, you can observe that:

• This matrix is diagonal - thus it is equal to its adjoint (conjugate transpose) and is hence Hermitian.
• It being diagonal also signifies that the computational basis vectors are its eigenvectors - For example [0 1 0 0 0 0 0 0]^T is an eigenvector of this matrix and corresponds to the cut 001 in Table 1. Refer to the below to get the mapping:
  • [1 0 0 0 0 0 0 0]^T: 000
  • [0 1 0 0 0 0 0 0]^T: 001
  • [0 0 1 0 0 0 0 0]^T: 010
  • [0 0 0 1 0 0 0 0]^T: 011
  • [0 0 0 0 1 0 0 0]^T: 100
  • [0 0 0 0 0 1 0 0]^T: 101
  • [0 0 0 0 0 0 1 0]^T: 110
  • [0 0 0 0 0 0 0 1]^T: 111
• Furthermore, the eigenvalues of these eigenvectors are actually the elements of the matrix - this is because the matrix is diagonal. For eg. The eigenvalue of [0 1 0 0 0 0 0 0]^T is 1 (row 1, column 1), which is what the value of 001 in Table 1 is. Similarly you can observe that the eigenvalue of [0 0 0 1 0 0 0 0]^T (011) is 2. You can try the same for the rest of the eigenvectors and thus realize that this particular matrix somehow represents the cost function for the problem instance shown in Figure 1 - where the input is the eigenvector and the output is the eigenvalue. We can find such matrices in general for any MaxCut problem (as explained below), and the problem is now translated into finding the eigenvector corresponding to the highest eigenvalue in such a matrix. However, note that this 8*8 matrix is for an elementary example of a graph having just 3 nodes. With higher number of nodes, it becomes intractable to calculate this matrix classically.

To find such matrices in general, let the cost function Hamiltonian be C, which is defined as:

\(\begin{equation}\label{eq:problemHamiltonian} C = \sum_{\langle jk \rangle}^{} C_{\langle jk \rangle} \end{equation}\) [1]

where ⟨jk⟩ represents an edge between vertex j and k in the graph, and,

\(\begin{equation} C_{\langle jk \rangle} = \frac{1}{2} (- \sigma^{z}_{j} \sigma^{z}_{k} + 1) \end{equation}\) [1]

The example shown in Figure 1 would have the following C. Since there are two edges in the graph:

1. \[C_{\langle 12 \rangle} = \frac{1}{2} (III - ZZI)\] \[= \frac{1}{2} \left( \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right)\] \[= \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\]
2. \[C_{\langle 13 \rangle} = \frac{1}{2} (III - ZIZ)\] \[= \frac{1}{2} \left( \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \right)\] \[= \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}\]

This would make

\[C = C_{\langle 12 \rangle} + C_{\langle 13 \rangle}\] \[\begin{equation} \hspace{20pt}= \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}\]

This is precisely the same matrix that we looked at before.

Finding the eigenvector corresponding to the highest eigenvalue

To summarize, if anyone gives us an arbitrary MaxCut problem, we now know how to create a Hamiltonian, such that finding the highest eigenvalue eigenvector will give us the solution to the problem.

We have just translated the problem into another mathematical form, but we still need some method or algorithm to find out which eigenvector corresponds to the highest eigenvalue. Note that this is still a difficult task because just with 3 qubits, we need an 8x8 matrix. For n qubits, we will need 2ⁿx2ⁿ matrix which is difficult to construct classically, let alone finding good eigenvectors after the construction. See this video for some great explanations, whis is what I referred to.

One way of finding the max eigenvalue eigenvector is using the Quantum Adiabatic Algorithm (QAA). QAA is a way of designing solutions for problems based on adiabatic evolution of quantum systems [2]. It comes from the Quantum Adiabatic Theorem [3] which states that a physical system that is initially in its ground state, tends to stay in this lowest energy state, provided that the Hamiltonian of the system is changed slowly enough. This is also true for any eigenstate of the system. QAA essentially states that an unknown ground state of an particular target Hamiltonian can be found by starting from a known ground state of another Hamiltonian, and slowly evolving this Hamiltonian into the target Hamiltonian across time. This is important because many problems can be represented by a Hamiltonian in such a way that finding the ground state of that Hamiltonian would give the optimal solution to that problem. The following would be the equation representing QAA:

\[H(t) = \left(1 - \frac{t}{T}\right)B + \left(\frac{t}{T}\right)C\]

where,

• B is a known Hamiltonian
• C is the problem Hamiltonian
• t is time, with H(t) representing the Hamiltonian of the system at time t
• T is the total run time of the algorithm

such that if we know the highest energy eigenstate |s⟩ of B, we will get the highest energy eigenstate of C by starting the evolution from state |s⟩ and keeping the total runtime T large. The states |011⟩ and |100⟩ are both equivalent and correspond to the eigenvalue 2 in the above example. The Quantum Adiabatic Algorithm requires a long running time, and for subexponential runtimes, it can get trapped in a false minimum [1].

The Quantum Approximate Optimization Algorithm (QAOA) proposes a different approach involving the following transformations to solve the problem:

\[| \gamma, \beta \rangle = U(B, \beta_p) U(C, \gamma_p) ... U(B, \beta_1)U(C, \gamma_1) | s \rangle\]

where,

• The start state \(| s \rangle\) is a uniform superposition over all the computational basis states. \(| s \rangle = \frac{1}{\sqrt{2^n}} \sum_{z}^{} | z \rangle\)
• C is the Problem Hamiltonian explained in the above section.
• The gate \(U(C, \gamma)\) is defined as:

\[U(C, \gamma) = e^{-i\gamma C} = \prod_{\langle i, j \rangle} e^{-i\gamma C_{\langle i, j \rangle}}\]

• B is a Mixer Hamiltonian, given by: \(B = \sum_{j=1}^{n} \sigma^x_j\) where \(\sigma_j^x\) is the Pauli X gate acting on the j-th qubit. An important property is that the Mixer Hamiltonian B does not commute with the Problem Hamiltonian C. If this were not the case, all the unitary operators would commute through leading to just one operator.

---

Commutativity of Operators of the Form $$e^A$$ For two time evolution operators to commute, the individual Hamiltonian operators should also commute. That is, the equality $$ e^{A} e^{B} = e^{A+B} = e^{B}e^{A}$$ holds only if Hermitian matrices A and B commute ([A, B] = 0). This is relevant since the Unitary Opeartors in QAOA are of the form of exponentials.

---

• \[U(B, \beta) = e^{-i\beta B} = \prod_{j=1}^n e^{-iB \sigma^x_j }\]
• \(\gamma \equiv \gamma_1 ... \gamma_p\) and \(\beta \equiv \beta_1 ... \beta_p\) are angles (real valued variables that parameterize our quantum circuit). The angles have to be chosen such that the algorithm converges to a good approximate solution.
• p denotes the number of layers in the circuit. There are p angles each for the problem and mixer Hamiltonians, leading to a total 2p angles that parameterize the circuit.

After applying p layers of the alternating gates, we get the state |\(\gamma, \beta \rangle\). Since C is a diagonal matrix, its eigenkets are the computational basis states. Hence, on performing a measurement in the computational basis state, we get an output state of the qubits |\(V_1 V_2 V_3 ... V_n \rangle\) where \(V_1, V_2, V_3 ... V_n \in {0, 1}\). Let the string z denote the this state \(V_1 V_2 V_3 ... V_n\). It is now ‘easy’ to calculate C(z) i.e. the value of the cut because all that one has to do is group the nodes and iterate over the edges to find out if the nodes are in opposite sets. Thus the value of a cut can be found in polynomial time - O(|E|). Each string z will correspond to a eigenvalue of C which can be easily calculated classically. Thus, on repeated measurements, we can map the values of z to C(z) and get the expectation value \(F_p\), denoted by:

\begin{equation}\label{eq:expectationvalue} F_p(\gamma, \beta) = \langle \gamma, \beta | C | \gamma, \beta \rangle \end{equation} The expectation value depends on the angles \(\gamma \equiv \gamma_1 ... \gamma_p\) and \(\beta \equiv \beta_1 ... \beta_p\). This expectation value needs to be maximized to get a good value of the cut which is close to the maximum value. This would require finding good parameters \(\gamma\) and \(\beta\) that maximize \(F_p\). The parameters are modified classically using different optimization techniques.

The Algorithm can be summarized as:

• Decide on the number of layers p, and some angles (\(\gamma, \beta\)).
• Start with a uniform superposition over all states, apply the gates and perform sample the results to get an expectation value.
• Optimize the parameters (\(\gamma, \beta\)) classically and repeat this process until \(F_p\) is maximized.

Analysis - Why does the algorithm work?

Consider the example in Figure 1 for analyzing the algorithm. The problem Hamiltonian is constructed above as well for this instance. The first gate that would be applied to the uniform superposition \(| s \rangle\) is \(U(C, \gamma_1) = e^{i\gamma_1 C}\). Since the problem Hamiltonian is always a diagonal matrix, from this would imply that the gate can be expressed as:

---

If a matrix is diagonalizable, then applying a function to the matrix corresponds to applying the function to the diagonal elements individually (in the basis in which the matrix is diagonal). This is because the function can be written as a Taylor series and multiplying the matrix by itself would just be equivalent multiplying the diagonals with themselves, and the Taylor series can be expressed in the diagonal elements individually. More specifically, we will use the following property: \[ \text{Let A = } \begin{bmatrix} d_1 & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & d_n \end{bmatrix} \text{be a n*n matrix} \] \[ e^A = I + A + \frac{A^2}{2!} + ... = \begin{bmatrix} 1 & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & 1 \end{bmatrix}+ \begin{bmatrix} d_1 & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & d_n \end{bmatrix} + \frac{1}{2!} \begin{bmatrix} d_1 & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & d_n \end{bmatrix} \begin{bmatrix} d_1 & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & d_n \end{bmatrix} + ... \] \[ = \begin{bmatrix} 1+d_1 + \frac{d_1}{2!} + ... & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & 1+d_n + \frac{d_n}{2!} \end{bmatrix} \] Thus, \begin{equation} e^A = \begin{bmatrix} e^{d_1} & 0 & 0\\ 0 & ... & 0 \\ 0 & 0 & e^{d_n} \end{bmatrix} \end{equation}

---

\[\begin{equation} U(C, \gamma_1) = \begin{bmatrix} e^{0\gamma_1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & e^{1\gamma_1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & e^{1\gamma_1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & e^{2\gamma_1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & e^{2\gamma_1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & e^{1\gamma_1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & e^{1\gamma_1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & e^{0\gamma_1} \end{bmatrix} \end{equation}\]

Thus, when this gate is applied to the state \(| s \rangle\), it will change the phase of the basis states according to how well they would solve the problem. Hence, the phase change of the states \(| 011 \rangle\) and \(| 100 \rangle\) would be greater than that of the rest. This gate hence encodes the solution in the phase of the individual computational basis states of the overall superposition. However, since this is purely a phase change of the complex number associated with the amplitude, the magnitude of the probability amplitudes would still remain the same. On performing a measurement, the probabilities of measuring states would still be equal to that in state \(| s \rangle\). The Mixer Hamiltonian then translates the change in phase to a corresponding change in the magnitude of probability amplitudes. However, to do this, a good value of \(\beta\) is still required. This is exactly why the classical optimization is required. See this video for a great visual explanation.

\[\begin{equation} B = XII + IXI + IIX \end{equation}\]

It can be trivially shown that all of the terms of B (XII, IXI, and IIX) commute with each other. Furthermore, B does not commute with C, which helps in escaping a local minima. After some evolutions, if a particular state ends up being an eigenstate of C, then in the absence of B, the state of the system will be stuck at the same eigenstate as \(e^{-i \gamma C} | Q \rangle = | Q \rangle\), if \(| Q \rangle\) is an eigenstate of C. If B and C commute, then they have the same eigenstate, and to make the trial state not get stuck, B needs to be chosen such as to not commute with C.

Following the expectation value expressed above (\(F_p\)), let \(M_p\) be the maximum possible expectation value over all angles for p layers.

\[\begin{equation} M_p = \text{max}_{\gamma, \beta} F_p(\gamma, \beta) \end{equation}\]

At layer p, if \(\gamma_p\) and \(\beta_p\) are set to 0, then the maximum possible expectation value would be the same as the maximum possible expectation value for p-1 layers. Thus the maximum possible expectation value for p layers would be greater than or equal to that of p-1 layers. Even if we can’t find better angles at the p-th layer, \(\beta_p, \gamma_p\) can be set to 0, which would yield the same maximum expectation value as with p-1 layers.

\[\begin{equation}\label{constrainedOptimization} M_{p} \geq M_{p-1} \end{equation}\]

QAOA is a trotterized approximation to the Quantum Adiabatic Algorithm [1] , where the sum of all angles \(\gamma\) and \(\beta\) is the total run time. For this approximation to hold, \(\beta\) and \(\gamma\) must be small, and since QAA requires a large runtime, p must be large.

---

Trotterization helps approximate exponentials of matrices when the matrices don't commute with each other [4]. Let $$e^{A+B}$$ be the exponential to be evaluated. $$ \begin{equation} e^{A+B} = \lim_{n\to\infty} (e^{A/n}e^{B/n})^n \end{equation} $$ See this video for an explanation.

---

Thus,

\[\begin{equation} \lim_{x\to\infty} M_p = max_z C(z) \end{equation}\]

This completes the brief explanation of why QAOA works. I hope you liked it. Feel free to contact me regarding anything about the post. In subsequent posts, I will be covering implementing this algorithm in CUDA-Q and Qiskit, how Qiskit comes up with the circuit and plotting the changing amplitudes and phases as in the video linked above. I will also try and explain how the classical optimization of the angles work in detail. Stay tuned!

---

References

---

[1] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. “A quantum approximate optimization algorithm”. In: arXiv preprint arXiv:1411.4028 (2014).
[2] Edward Farhi et al. “Quantum computation by adiabatic evolution”. In: arXiv preprint quantph/0001106 (2000).
[3] M. Born and V. Fock. “Beweis des Adiabatensatzes”. In: Zeitschrift f¨ur Physik 51.3 (1928). ID: Born1928, pp. 165–180. url: https://doi.org/10.1007/BF01343193.
[4] Grant Kluber. Trotterization in Quantum Theory. 2023. arXiv: 2310.13296 [quant-ph]. url: https://arxiv.org/abs/2310.13296.